 When using the Geometer's Sketchpad it is often better to "start from sketch, not from scratch". That is, give students a premade sketch rather having them build something from nothing (as many textbooks would have you do).
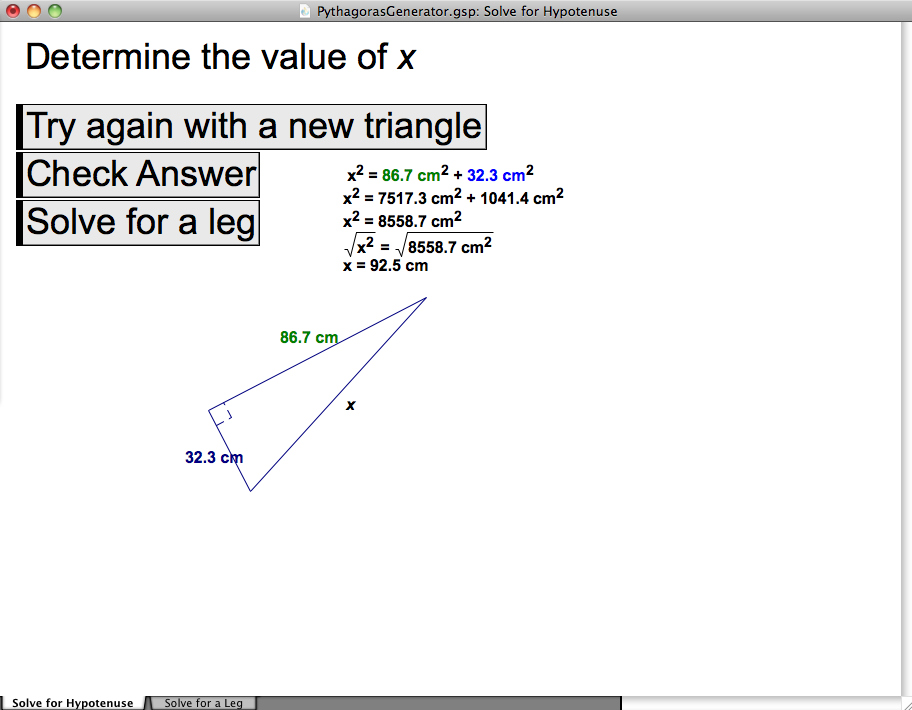
When using the Geometer's Sketchpad it is often better to "start from sketch, not from scratch". That is, give students a premade sketch rather having them build something from nothing (as many textbooks would have you do). In this activity students can download a GSP sketch that allows them to practice determining the hypotenuse (on the first page) or a leg (on the second page). The sketch will generate an infinite number of questions and give a full solution for each.
Note: Although Pythagorean Theorem is introduced in grade 8, it is only supposed to be relating more to the area model so these practice problems may not fit that.
- MPM1D, MFM1P: D, C2.2 - solve problems using the Pythagorean theorem, as required in applications
- MPM2D, MFM2P: C,A2.2 - determine the measures of the sides and angles in right triangles, using the primary trigonometric ratios and the Pythagorean theorem;
- All that is needed are the electronic downloads (below)
- Note that this really works well on an iPad using the Sketchpad Explorer App (which is free)
- You can also use this on any web based computer (or Chromebook) with this Web sketch
- Pythagoras_Generator.gsp
- Web sketch here
- For more sketches like this go to my full page





